MATHEMATICS
Concept-Practice Framework
Our carefully curated notes and worksheets aim to break down concepts from textbooks into easily digestable bite-sized parts and arrange activities according to cognitive levels. Our curriculum is conceptually designed step-by-step such that our worksheets follow a progressive learning curve and the learning objectives of each topic closely. This enables students to grasp new concepts more easily and tackle challenging problems with confidence. Our step-by-step approach aids weaker students in building a strong foundation.


JustEdu students get to try their hand at every single math concept ever tested in school. We will train our students to tackle higher order questions via Heuristics Training and Challenging Word Problems.
Our heuristics training challenges our students to a wide variety of questions that requires them to think out-of-the-box. They will be able to handle questions such as:
Give a Representation (Diagram Drawing, Making a List, Use Equations)
Make a Calculated Guess (Guess & Check, Patterns, Making Assumptions)
Working out the Process (Act it out, Working backwards, Before and After)
Changing the Problem (Restate the Problem, Simplifying the Problem, Solve Part of the Problem)
Other popular word problems typically come from a selected range of topics like: Ratio, Rate, Fractions, Percentage, Volume, Speed. These problems sums specifically tests a student's spatial visualisation skills and application which requires practice and most importantly, tutorial guidance.
Our teachers are thoroughly trained and equipped with detailed worked solutions to guide students through each step of the problem.
Logical reasoning and multiple-concept questions involve real life applications and requires students to break down a word problem into multiple concept parts to activate relevant knowledge. Requiring the initial help of our tutors to help students visualise the problem, students will progressively activate and link their knowledge of various concepts, grasping a bird's eye view of the problem to work their way towards the solution.

TEACHING APPROACH
When it comes to teaching methodology, we look towards developing the 5 'E's in each of our students. These are the five key tenets of our approach to Education.
ENGAGE
Here, we engage our students and grab their attention before we start going through the topic by sharing with them:
How the topic they are about to learn can be applied in real life
History of Mathematics (Secondary)
Discussions based on the students' initial understanding of the topic to make connections between past and present learning experiences
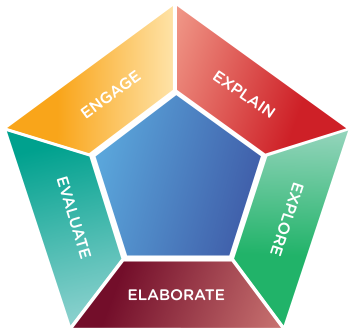
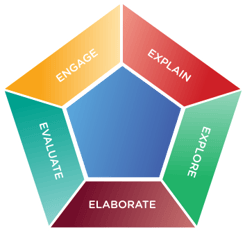
EXPLAIN
Once we have gained our students' attention, we start to:
Explain the concepts involved in the everyday applications and the videos or flash applets used
Determine levels of understanding and identify possible misconceptions
This is done via the use of our specially designed Just Mathematics notes
EXPLORE
Next, we get them directly involved with the topic and materials and start on their exploratory journey by:
Conducting Exploratory Activities
Allowing students to interact with Flash applets or videos specially selected to invoke students' interest and at the same time educate them
ELABORATE
EVALUATE
Here we extend our students' understanding by:
Expanding on the concepts they have learned
Making connections to other related concepts
Applying their understanding to the world
Finally, at the end of the lesson, we evaluate our students' understanding via the following:
Checking of answers
Evaluation of students' workings and correction of misconceptions
Clarification of common misunderstanding of concepts
Reinforcement of concepts
Recapitulation based on the students' unique needs
This is done by exposing them to:
Real world application questions
Contextual questions
Specially adapted questions based on concepts tested in schools and national exams
CURRICULUM SAMPLES
Lower Secondary
A contractor agrees to lay a road of length 3000 m in 20 days. He employs 80 men who work 8 hours a day. After 15 working days, he finds that only 2000 m of the road is completed. How many more men should he employ so as to finish the work on time if each man now works 10 hours a day?
Show Solution
No. of hours worked in 15 days
= 8 x 5
= 120
Remaining no. of hours to work
= 5 x 10
= 50
Remaining length of road to lay
= 2000 - 1000
= 1000 m
Let the number of workers be x and the total number of hours be y. Since the number of workers is inversely proportional to the total number of hours,


Let the number of workers be x and the total length of road be I. Since the number of workers is directly proportional to the length of road,


Therefore, 96 - 80 = 16 more men required.
Gillian and Cadence packed 4000 presents for an orphanage.
The time Gillian took to pack 7 presents was similar to the time Cadence took to pack 9 presents.
They earned 45¢ for every present packed. An additional $1.50 was earned for every 30 presents packed.
How much more did Cadence earn than Gillian?
Show Solution
4000 ÷ (7 + 9) = 250
250 x 7 = 1750
250 x 9 = 2250
1750 x 45¢ = $787.50
1750 ÷ 30 = 58 R 10
$787.50 + 58 x $1.50 = $874.50
2250 x 45¢ = $1012.50
2250 ÷ 30 = 75
$1012.50 + 75 x $1.50 = $1125
$1125 - $874.50 = $250.50
Ans: $250.50
Upper Secondary
In a bridge structure, the mast above each pillar is 87 metres high.
The gradient at which the longest steel cable is connected to the centre of the bridge is such that the ratio of vertical distance : horizontal distance is 29 : 57.




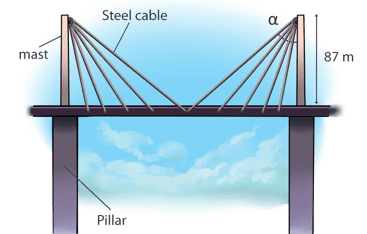
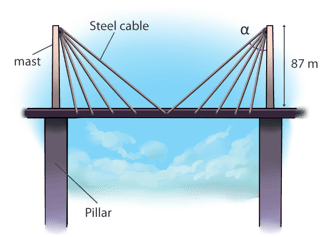
a) Show that the angle, α, is 63.03° correct to 2 decimal places.
b) Calculate the length of 2 pieces of the longest steel cable attached from the top of the mast to the centre of the bridge.
Show Solution
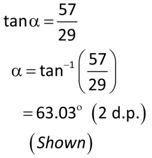
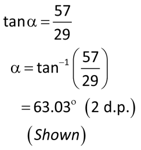
a)
b)


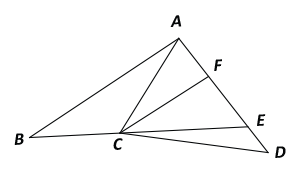
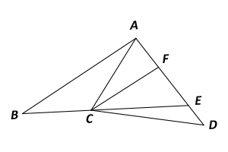
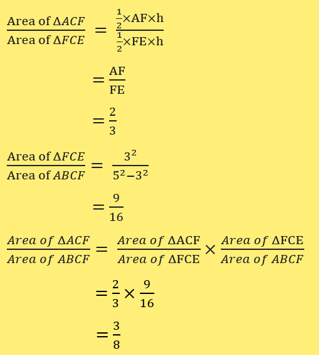
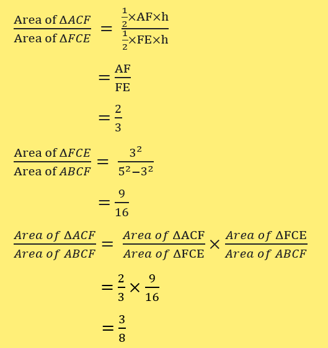
In the diagram, ΔFCE is similar to ΔABE. Given that ΔABC has an area of 24 cm2, 3BC = 2CE and 4DE = DA,
a) find the area of ΔACE;
b) find the area of ΔFCE;
c) show that area ΔCDE = ½ area of ΔABC;
d) find the value of area of ΔACF
area of ABCF
Show Solution
a)
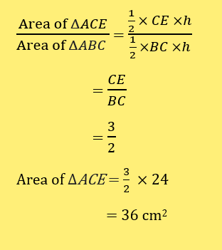
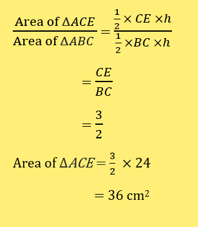
b)
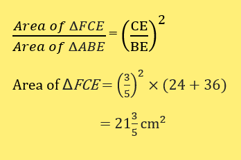
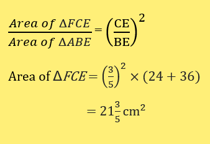
c)

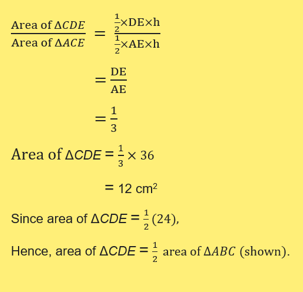
d)
At JustEdu, we are committed to providing top-tier mathematics tuition across Singapore, catering to students from primary levels through junior college. Our math tuition centres offer a comprehensive range of programmes, including primary mathematics tuition, secondary math tuition, and maths classes for junior college students. If you're searching for "mathematics tuitionnear me" or "math tuition centre," JustEdu is your ideal choice.
Concept-Practice Framework
Our unique Concept-Practice Framework is designed to break down complex mathematical concepts into easily digestible segments. This structured approach ensures that students build a solid foundation, enabling them to tackle hallenging problems with confidence. For those seeking "math enrichment classes," our curriculum offers progressive learning that aligns with educational objectives.
Heuristics Training and Challenging Word Problems
We emphasize heuristics training, encouraging students to think critically and approach problems from various angles. Our programme includes exposure to higher-order questions and challenging word problems, particularly in topics like ratio, rate, fractions, percentage, volume, and speed. This method enhances spatial visualization skills and problem-solving abilities, essential for excelling in mathematics.
Dedicated and Experienced Educators
Our team of passionate educators is thoroughly trained and equipped with comprehensive step by step solutions to effectively guide students through each problem-solving step. Their dedication ensures that learners receive personalized attention, fostering an environment where students can thrive in their mathematical pursuits.
Comprehensive Programmes Across Multiple Locations
JustEdu offers a wide array of programmes, including primary mathematics tuition, secondary math tuition, and maths classes for junior college students. With multiple centres strategically located, finding "math tuition near me" is convenient for all students in Singapore.
Complimentary Class
To experience our teaching methodology firsthand, we invite you to attend a complimentary class. This opportunity allows prospective students to understand how our programmes can cater to their specific needs and academic goals. Choose JustEdu for your mathematics tuition needs and empower your child with the skills and confidence to excel academically.
